Dreiecke |
| 01.07.2003, 17:42 | JACKtheRIPPER | Auf diesen Beitrag antworten » | ||||
| Dreiecke bin neu hier 
Kann mir jemand sagen wie man den Flächeninhalt eines Dreiecks berechnet 
Und wie man das Volumen eines Dreieckes berechnet. Ausserdem müsste ick noch wissen wie man den Flächeninhalt und das Volumen eines Prismas berechnet.
Danke Jenny |
||||||
| 01.07.2003, 17:46 | Kontrollator | Auf diesen Beitrag antworten » | ||||
| RE: Dreiecke lol Flächeninhalt eines Dreickes: Grundseite*höhe durch 2 oder? 
im Matheboard |
||||||
| 01.07.2003, 17:47 | Thomas | Auf diesen Beitrag antworten » | ||||
hi
also den flächeninhalt eines dreiecks berechnest du ganz einfach mit 1/2 * Grundseite * Höhe oder einfach gesagt 1/2 * g * h. ein dreieck ist 2-dimensional, darum hat es auch kein volumen.
das volumen eines prismas: du nimmst ganz einfach das dreieck, das du vorne hast bei einem prisma und berechnest dessen fläche mit 1/2 * g * h. und dann multiplizierst du das ganz einfach mit der länge des prismas. einigermaßen kapiert? ich hoffe ich hab auch alles richtig erklärt 
|
||||||
| 01.07.2003, 17:52 | JACKtheRIPPER | Auf diesen Beitrag antworten » | ||||
Habs jetzt einigermaßen verstanden, Danke. :] Kennt jemand im Netz vielleicht einige Übungsaufgaben? |
||||||
| 01.07.2003, 17:53 | jama | Auf diesen Beitrag antworten » | ||||
hi jenny, volumen eines dreiecks kann man nicht berechnen: ein dreieck ist 2 dimensional
mit flächeninhalt eines prismas meinst du woh den oberflächeninhalt. und meinst du auch ein regelmäßiges dreiseitiges prisma? oder ein regelmäßiges sechsseitiges prisma? oder ganz wat anderes. 3seitiges: A = oberflächeninhalt V = volumen a = die kantenlänge des mit einbeschriebenen dreiecks |
||||||
| 01.07.2003, 17:56 | jama | Auf diesen Beitrag antworten » | ||||
grml, jetzt sind mir diese beiden pappnasen zuvor gekommen X( :rolleyes: :P hier mal eine übungsaufgabe: die oberfläche eines geraden prismas mit dem volumen 72 cm³ beträgt 168 cm². die grundfläche hat einen flächeninhalt von 12cm². berechne die höhe des prismas und den umfang der grundfläche
viel spass damit 
nachtrag: Ein gerades dreiseitiges Prisma hat lauter gleich lange Kanten. Bestimme die Kantenlänge (auf mm genau) so, dass die Prismenoberfläche 10 m2 beträgt. |
||||||
| Anzeige | ||||||
|
|
||||||
| 01.07.2003, 18:32 | JACKtheRIPPER | Auf diesen Beitrag antworten » | ||||
Hallo, danke für Eure Antworten. Hier ein Ausschnitt aus meinen Buch, ich bräuchte Hilfe bei den Aufgaben 2 * Nr.1-3 3 * Nr. 1 Wäre gut wenn Ihr mir beschreiben könntet was Grundseite usw. ist. Danke |
||||||
| 01.07.2003, 19:42 | Thomas | Auf diesen Beitrag antworten » | ||||
hi, also bei den ** die nummer 1: du musst das ganze ganz einfach in 2 verschiedene flächen aufteilen, ein rechteck und oben das dreieck, beide flächen ausrechnen und zusammenzählen. die fläche das rechtecks = 8,20 * 3,20 m² (also grundseite mal höhe) und die fläche des dreiecks oben = (8,20 * 2,50) / 2 m² also die grundseite mal die höhe des dreicks geteilt durch 2. bei der *** die nummer 1: auch hier gilt wieder die aufteilung in "einfache" flächen. berechne zuerst das große rechteck unten: 4,00 * (3,50 + 5,00) m² diesmal die höhe mal die grundseite... dann die beiden dreiecke oben: links: (1,80 * 3,50) / 2 m² rechts: (1,80 * 5,00) / 2 m² und jetzt müssen wir noch das dreieck unten rechts abziehen: 1,30 * (3,50 + 5,00) m² zusammenzählen bzw. abziehen und du hast das endergebnis... prinzip verstanden bei den beiden 1er aufgaben? |
||||||
| 01.07.2003, 20:15 | jama | Auf diesen Beitrag antworten » | ||||
Aufgabe 1 Die Giebelwand des Hauses soll gestrichen werden. Wie groß ist die Fläche?  Lösung: Die Wand setzt sich aus 2 Formen zusammen. Einmal aus einem Rechteck und einmal aus einem Dreieck (s. Bild)  Wie du siehst haben die Seiten des Rechtecks die Maße 8,20 meter und 3,20 meter. Für die Fläche des Rechtecks ergibt sich dann: 8,20m * 3,20m = 26,24 m². Um die Fläche der gesamten Giebelwand herauszufinden, müssen wir auch noch die Fläche des Dreiecks dazu addieren: Grundseite des Dreiecks: g = 8,2m Höhe des Dreiecks: h = 2,5m è ½ * g * h = Fläche des Dreiecks: è ½ * 2,5 * 8,2 = 10,25m² Für die Fläche der Wand ergibt sich also: 10,25m² + 26,24m² = 36,49m² Aufgabe 2 Berechne die Fläche A1 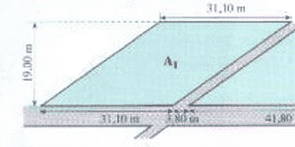 Lösung: Es handelt sich hier um ein Parallelogramm. Wenn man das Parallelogramm halbiert, erhält man 2 gleichgroße Dreiecke.  Um die Fläche eines Dreiecks zu berechnen, muss man ja ½ * g * h rechnen. Also muss man, um die Fläche eines Parallelogramms zu errechnen (= 2 gleichgroße Dreiecke), 2 * ½ * g * h = g * h rechnen. In diesem Beispiel heißt das: 19,00m * 31,10m = 590,9m² Aufgabe 3 Berechne das Volumen 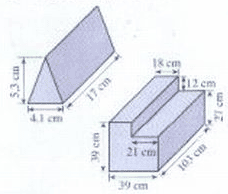 das volumen eines prismas: du nimmst ganz einfach das dreieck, das du vorne hast bei einem prisma und berechnest dessen fläche mit 1/2 * g * h. und dann multiplizierst du das ganz einfach mit der länge des prismas. Also: (½ * 4,1 * 5,3) * 17 = 184,705cm³ Der 2. Körper besteht aus 2 aufeinander gesetzten Quadern. Kleiner Quader: 18cm * 12cm * 103cm = 22248cm³ Großer Quader: 39cm * 21cm * 103cm = 84357cm³ Körper = Großer + Kleiner Quader = 22248cm³ + 84357cm³ = 106602cm³ |
||||||
| 01.07.2003, 21:44 | jama | Auf diesen Beitrag antworten » | ||||
wieso machst aus dem oberen dreieck 2 dreiecke bei der letzten aufgabe? |
||||||
| 01.07.2003, 22:56 | Thomas | Auf diesen Beitrag antworten » | ||||
hm, keine ahnung, weil ich doof bin vielleicht? :P nein, scheiß stress, erst für kunst so ein dummes logo machen, ansonsten reißt mir der lehrer morgen den kopf ab, da hab ich au nix tolles zusammengekriegt, nur ne simple fotomontage, dann hatt ich auch noch nachmittag heute, dann ist die mathehausi so schwer, und ich muss auf morgen noch > 20 seiten geschichte lernen... alles ausreden ich weiß
|
||||||
| 22.08.2003, 23:01 | Tristan | Auf diesen Beitrag antworten » | ||||
Hi, dacht eigentlich, ich würde hier schnell mal die übriggebliebene Aufgabe lösen, bin aber auf ein Problem gestossen.
Wie bekomme ich ein Bild in meinen Text??? Gibt zwar einen schönen Button "Bild einfügen" aber was muss ich in die auftauchende Befehlsleiste eingeben? |
||||||
| 23.08.2003, 04:10 | Thomas | Auf diesen Beitrag antworten » | ||||
die url zum bild natürlich
|
||||||
| 23.08.2003, 15:09 | jama | Auf diesen Beitrag antworten » | ||||
ansonsten kannste auch ein bild im anhang speichern. wenn du einen neuen beitrag verfasst, einfach auf "bearbeiten ..." in der Zeile "Dateianhang" klicken und das bild auf deiner festplatte auswählen
|
||||||
| 23.08.2003, 18:24 | Tristan | Auf diesen Beitrag antworten » | ||||
Na dann probier ich es einfach mal: Ich hab den Körper einfach in ein Quader und ein Prisma zerlegt. Somit ergibt sich für das Volumen: Quader: V=a*b*c =9cm*8cm*21cm =1512cm³ Prisma: V=g*h =9cm*6cm/2 *21cm =567cm³ Jetzt beide addieren V=2079cm³ Für die Oberfläche betrachtet man am besten Fläche für Fläche: Grundfläche: 14cm*21cm=294cm² Seitenflächen: 9cm*21cm+10,8cm*21cm=415,8cm² Fläche oben: 8cm*21cm=168cm² Vorne und hinten: 2*9cm*8cm+9cm*6cm=198cm² Also A=1075,8cm² So war jetzt sehr ausführlich und hab festgestellt, dass die Aufgabe gar nicht gebraucht wurde. Na ja war halt ne kleine Übung. |
||||||
| 23.08.2003, 19:14 | jama | Auf diesen Beitrag antworten » | ||||
gebrauchen kann man das immer. kann ich deine lösung in die tipps und tricks kategorie eintragen? |
||||||
| 23.08.2003, 23:25 | Tristan | Auf diesen Beitrag antworten » | ||||
Klar doch, sollen so viele wie möglich davon profitieren in der Hoffnung, dass irgendwann jeder Spass an Mathematik hat. :] |
||||||
| 24.08.2003, 03:07 | jama | Auf diesen Beitrag antworten » | ||||
wunderbar, dann werd ich das mal machen
|
||||||
| 19.06.2004, 21:50 | emeli | Auf diesen Beitrag antworten » | ||||
| Was sind Kathteten? :P Hi bin neu hier und hab ne Frage : was sind Kathten? danke |
||||||
| 19.06.2004, 21:53 | Poff | Auf diesen Beitrag antworten » | ||||
| RE: Was sind Kathteten? Die beiden kürzeren Dreiecksseiten (die den rechten Winkel bilden) im rechtwinkligen Dreieck . |
||||||
| 19.06.2004, 21:56 | emeli | Auf diesen Beitrag antworten » | ||||
| Hilfe ich komme nicht weiter :P Hallo. kann mir bitte jemand helfen!! was sind Katheten? Danke sagt Emeli |
||||||
| 19.06.2004, 22:09 | Emeli | Auf diesen Beitrag antworten » | ||||
| RE: Dreiecke Hi jenny, der Flächeninhalt eines Dreiecks Berechnet man so 
a*ha)/2 oder (b+hb)/2 oder (c*hc)/2 |
||||||
| 19.06.2004, 22:12 | Emeli | Auf diesen Beitrag antworten » | ||||
| Prisma
Wie rechnet man Das Volumen und die Grundfläche eines Prismas aus ????????? Danke Leute |
||||||
| 19.06.2004, 22:20 | Lyla | Auf diesen Beitrag antworten » | ||||
Dreieck
Wie ist die Innenwinkelsumme in einem Dreieck. Ich bin neu Könnt ihr mir bitte helfen Danke , ach ja und wie definiert man ein Dreieck eigentlich? |
||||||
| 19.06.2004, 23:23 | ChrisM | Auf diesen Beitrag antworten » | ||||
Jetzt stellt doch nicht so viele Fragen in einem uralten Thread.
Aber nun gut:
Kann man nicht allgemein sagen, was für eine Form soll die Grundfläche denn ahben? Volumen = Grundfläche * h, logisch, oder?
Laut dem Innenwinkelsummensatz ist die Winkelsumme in einem Dreieck immer und überall 180°, oder PI, wenn dus im Bogenmaß haben willst :P Wie definiert man ein Dreieck? Ein Vieleck mit drei Seiten, drei Innenwinkeln und drei Ecken :P |
||||||
| 20.06.2004, 00:29 | sommer87 | Auf diesen Beitrag antworten » | ||||
@emeli und Lyla: schaut dazu auch mal in die Tipps & Tricks ABteilung hier im Board. Für fragen, die nicht zum thema des threads passen, bitte beim nächsten mal einen neuen thread eröffnen. Danke
|
||||||
| 20.06.2004, 08:31 | johko | Auf diesen Beitrag antworten » | ||||
emeli,lyla: Auch mit verschiedenen Nicks wirst deine Absicht offenbar. Johko Ich schließe mal die Angelegenheit. |
||||||
|
|
Verwandte Themen
| Die Beliebtesten » |
|
| Die Größten » |
|
| Die Neuesten » |
